Quantum Mechanics #3- Classical Mechanics failed to explain Black Body Radiation, led Planck to the discovery
Quantum Mechanics #3
Black Body
A perfectly black body is one which absorbs totally all the radiation of any wavelength which fall on it. As it neither reflects nor transmits any radiation, it appears black; whatever be the colour of incident radiation. The main characteristic of such a body is that when heated to a suitable high temperature, it emits full or total radiation.
As it is a perfect absorber, it is also a perfect radiator, its emission being the greatest possible for every wavelength at any given temperature.
As it is a perfect absorber, it is also a perfect radiator, its emission being the greatest possible for every wavelength at any given temperature.
 |
| BLACK BODY |
Black Body in Practice
In practice, a perfectly black body is not available. Lamp-black and Platinum black are the nearest approach to a black body. However, a body showing close approximation to a perfectly black body can be constructed.
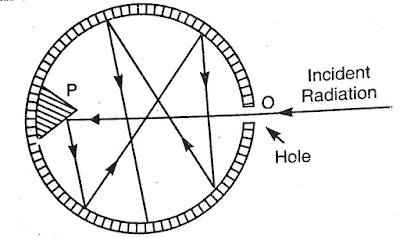 |
| Black Body absorber |
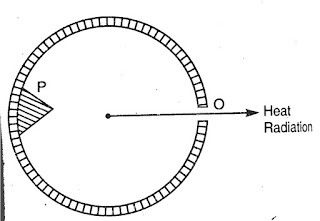 |
| Black body emitter |
A closed chamber, say a hollow sphere (known as hollow spherical cavity) whose inner surface is coated with platinum black or lamp black having a small opening O in the surface and a projection P opposite to the opening, acts as a black body.
It should be noted that perfectly black body is an ideal concept similar to a perfect gas which does not exist, i.e. it can not be 100% realized in actual practice. The platinum black surface absorbs 98% and lamp black 96% the incident radiation.
A body emits radiation when it is heated. The emitted radiation from the hot body is called thermal radiation. When a black body is heated, it emits more radiations per unit area than any other body at a particular temperature.
Since a perfectly black body absorbs all the radiation falling upon it , so it has absorptivity equal to 1. A perfectly black body has emissivity also equal to 1.
A body emits radiation when it is heated. The emitted radiation from the hot body is called thermal radiation. When a black body is heated, it emits more radiations per unit area than any other body at a particular temperature.
Since a perfectly black body absorbs all the radiation falling upon it , so it has absorptivity equal to 1. A perfectly black body has emissivity also equal to 1.
Fery's Black Body
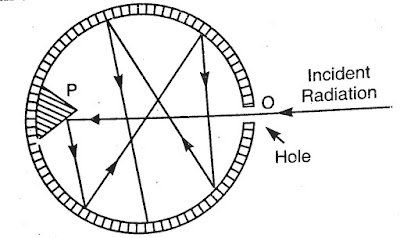 |
| Designed by Fery: black body absorber. |
A double walled hollow copper sphere is taken and coated with lamp black on its inner surface. A fine hole O acts as a very narrow opening. When the radiation enter through the narrow opening they suffer multiple reflections after falling on a pointed projection P which is made just in front of the hole.
After suffering multiple reflections, the radiation are completely absorbed. This body acts a a black body absorber.
Now , when this body is placed in a bath at a fixed temperature, the hear radiation come out of the hole, as shown in the figure below.
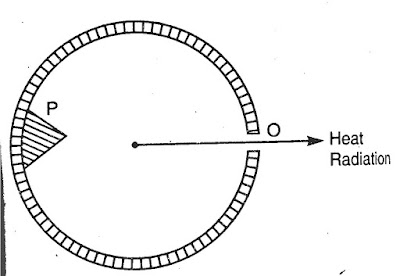 |
| Fery's black body emitter |
Wien's Black Body
Wien also constructed a black body in the form of cylinder. This black body is commonly used nowadays, as it is more convenient to use.
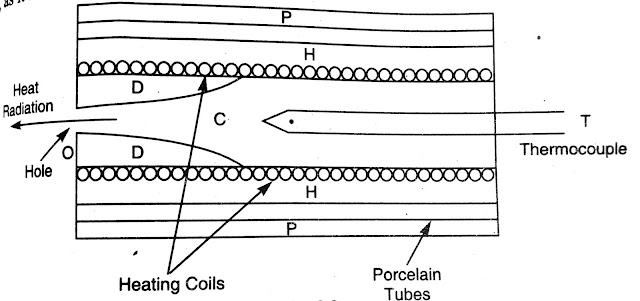 |
| Wien's Black Body |
It consists of a hollow cylindrical chamber C of brass or platinum having heating coil of thin platinjm wire HH wound over it. The cylinder is protected by co-axial porcelain tubes PP. When a suitable current is passed through the coil, the cylinder is heated to a desired temperature.
The inner surface of the chamber C is painted black, so that it reaches the equilibrium position in a small time. The radiation from the cylinder is limited by blackened concave duaphragms D and emerges out of the hole O. The temperature of the chamber is measured by the thermocouple T. The hole O will act as a black body radiator.
The inner surface of the chamber C is painted black, so that it reaches the equilibrium position in a small time. The radiation from the cylinder is limited by blackened concave duaphragms D and emerges out of the hole O. The temperature of the chamber is measured by the thermocouple T. The hole O will act as a black body radiator.
Distribution Of Energy in Black Body Spectrum
Lummer and Pringesheim investigated the distribution of energy among the radiation emitted by a black body at different temperatures.
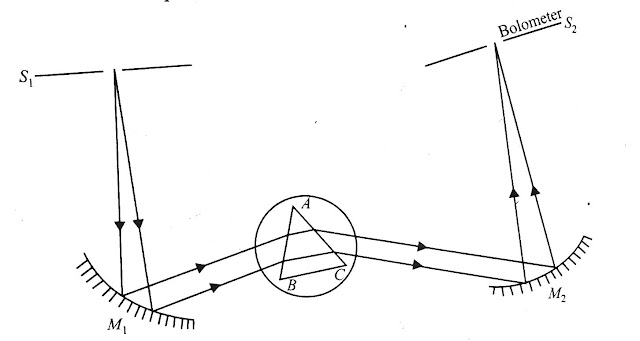
The experimental arrangement of Lummer and Pringesheim is shown in above figure. The radiation from a black body pass through the slit S1 and falls on thr reflector M1, which passes through rock-salt or fluorspar prism ABC kept on a lotating(turn) table of spectrometer. The emergent light is focused by the concave reflector M2 on a line bolometer placed behind the slit S2.
The bolometer is connected to a sensitive galvanometer. The turn table is slowly rotated so that the different parts of the radiation spectrum successively falls on thr bolometer and the corresponding deflection in galvanometer are recorded.
The intensity of each line is proportional to the deflection in the galvanometer. Then the curve is drawn between intensity and the wavelength(λ).
Then the body is heated to different temperatures and the curves are drawn for various temperatures. The curves obtained are -
Results. From the above curves, we can conclude that
1). At a given temperature the energy is not uniformly distributed in the radiation spectrum of a black body.
2). At a given temperature, the intensity of heat radiation increase in wavelength and at a particular wavelength its value is maximum. With further increase in wavelength, the intensity of heat radiation decreases.
3). An increase in temperature causes an increase in the emission for all wavelengths.
4) An increase in temperature causes a decrease in
λ(m), where λ(m) is the wavelength fot which the energy is maximum, such that
λ(m)T = constant
Explanation: By Classical Laws
There were two main explanations given. One is Wien's Law and the other one is Rayleigh-Jean's Law.
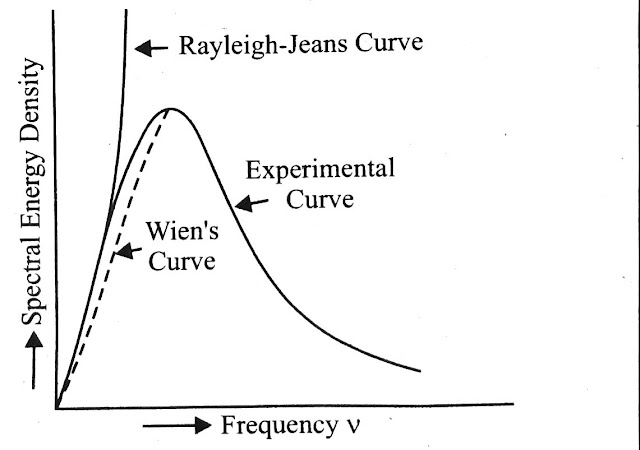
Wien's Law. The success of Wien's law is that it hold good only in the region of shorter wavelengths at lower temperatures. It does not hold good at longer wavelengths and higher temperatures.
Rayleigh-Jean's Law. The problem in this explanation is that the energy density will continuously increase with increase in frequency and approaches infinity (as shown in above graph).This is contradiction to observed results.
It is clear that, the energy distribution of a black-body
could not be explained on the basis of classical concept.
Quantum Explanation: Planck's Radiation Law
 |
| Max Planck |
The failure of classical mechanics led Planck(in1900) to the discovery that radiation is emitted in quanta.
For Planck's Quantum Theory visit- Planck's Quantum Theory
Planck's modified Rayleigh-Jean's Law with his assumption that a black body is associated with large mumber of harmonic oscillators.
Based on this he derived an equation, as shown below:
Above equation is called Planck's Radiation Law. This law can explain all the experimental results for black body radiation.
The failure of classical mechanics was a key in the discovery of quantum mechanics by Max Planck.
Click on the sidemenu and follow the blog!
Click on subscribe button for email subscription. You will get an email notification whenever a new post comes.
Share your feedback down in the comment box.
Thanks for reading!
Our facebook page- Know Physics Facebook Page
Our Quora space - Know Physics Quora space


Comments
Post a Comment
If you have any doubts or suggestions please kindly share.