STATISTICAL MECHANICS: A BRIEF HISTORY
Statistical mechanics was initiated in 1870 with the work of Austrian physicist Ludwig Boltzmann, much of which was collectively published in Boltzmann's 1896 lectures on gas theory. Statistical mechanics provided a molecular level interpretation of microscopic thermodynamic quantities such as eork, heat, free energy and entropy.
The study of statistical physics is mainly classified into categories. These are:
- Classical statistics or Maxwell-Boltzmann statistics.
- Quantum statistics or Bose -Einstein and Fermi-Dirac statistics.
STATISTICAL BASIS
Statistics is that branch of science which deals with the collection, classification and tabulation of numerical data as the basis of explanation, description and comparison of various phenomenon. When statistical concepts are applied to physics, the new branch that emerges is called statistical physics.
Statistical physics deals with macroscopic systems. i.e. the system consisting of a large number of individual particles such as atoms, molecules etc. It is not concerned with the behaviour of the individual particles of the system but takes into consideration the average or most probable properties of the system. As a system is a collection of a large number of particles of one type, we may have a system composed of atoms, molecules, protons, neutrons or electrons.
In certain cases, particularly where the system contains a large number of particles, ordinary laws of mechanics could not be used, as it is impossible to follow the motion of each particle. It is impossible to apply the ordinary laws of mechanics to a physical system containing large number of particles, particularly that of electrons. Such problems are however, successfully solved by statistical mechanics.
In certain cases, particularly where the system contains a large number of particles, ordinary laws of mechanics could not be used, as it is impossible to follow the motion of each particle. It is impossible to apply the ordinary laws of mechanics to a physical system containing large number of particles, particularly that of electrons. Such problems are however, successfully solved by statistical mechanics.
There are three statistics depending upon three different kinds of particles:
- Maxwell-Boltzmann statistics: This is applicable to the identical, distinguishable particles of any spin stop the molecules of a gas are the particles of this kind.
- Bose-Einstein statistics: This is applicable to the identical, indistinguishable particles of zero or integral spin. These particles are called bosons. Examples of bosons are Helium atoms at low temperature and the photons.
- Fermi-Dirac statistics: This is applicable to the identical, indistinguishable particles of half integral spin. These particles obey Pauli exclusion principle and are called fermions. Examples of fermions are electrons, protons, neutrons etc.
SOME BASIC TERMS OF STATISTICAL MECHANICS
(1) System
In statistical mechanics, the term system is used to represent system (or collection) of large number of small particles( such as atoms or molecules) with one or more than one independent part.
For example, if we have to distribute some particles in the boxes or to distribute some energy(or momentum) in some states, then the particles and the boxes or the energy(or momentum) and the states together, is called the system.
(2) Statistical Ensembles
Statistical mechanics, Gibbs introduce the concept of ensemble. An ensemble is defined as a collection of large number of macroscopically identical but essentially independent systems. Macroscopically identical means that each of the systems constituting an ensemble satisfies the same macroscopic conditions e.g., volume, energy, pressure, temperature, total number of particles etc. Independent systems means that the system constituting an ensemble are mutually non- interacting.
Kinds of Ensembles - According to Gibbs, there are three standard ensembles to which real experiments could be approximated. These are:
1. The Microcanonical ensemble
2. The canonical Ensemble, and
3. The Grand-canonical ensemble.
Grand-Canonical Ensemble- The Grand-canonical ensemble is a collection of systems having the same temperature T, volume V and chemical potential µ.
The walls are permeable and conducting. So both energy and particles can be exchanged.
Kinds of Ensembles - According to Gibbs, there are three standard ensembles to which real experiments could be approximated. These are:
1. The Microcanonical ensemble
2. The canonical Ensemble, and
3. The Grand-canonical ensemble.
Microcanonical Ensemble- The micocanonical ensemble is a collection of systems having the same energy E, volume V and number of particles N.
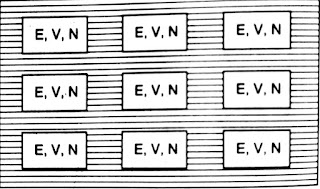 |
| Microcanonical Ensemble |
Canonical Ensemble- The canonical Ensemble is a collection of systems( independent) having the same temperature T, volume V, and number of identical particles N.
In canonical ensemble, systems can exchange energy but not the particles. There is an impermeable but conducting wall between systems.
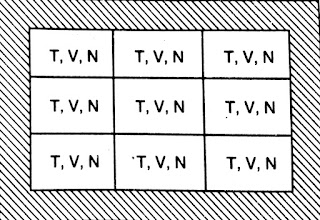 |
| Canonical Ensemble |
The walls are permeable and conducting. So both energy and particles can be exchanged.
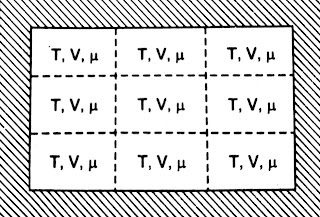 |
| Grand-canonical Ensemble |
(3) Macrostate
In statistical mechanics, the macrostate of a system is the state which can be experimentally observed. Consider 4 different particles. Let them be a,b,c and d.
We have two similar open boxes(compartments).
The possible ways by which 4 particles can be distributed in two compartments are shown in the table.
Thus, there are 5 different distributions (0,4), (1,3), (2,2), (3,1), and (4,0).
Each compartment wise distribution of a system of particles is known as a Macrostate.
In above example there are 5 macrostates - (0,4), (1,3), (2,2), (3,1), and (4,0).
In above example, we came to know that there are 5 macrostates for distribution of 4 particles in 2 boxes.
So if there are 'n' particles, which are to be distributed in 2 boxes, then there will be 'n+1' macrostates.
We have two similar open boxes(compartments).
The possible ways by which 4 particles can be distributed in two compartments are shown in the table.
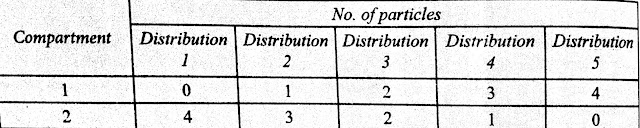 |
| Distribution of 4 particles in 2 compartments |
Each compartment wise distribution of a system of particles is known as a Macrostate.
In above example there are 5 macrostates - (0,4), (1,3), (2,2), (3,1), and (4,0).
In above example, we came to know that there are 5 macrostates for distribution of 4 particles in 2 boxes.
So if there are 'n' particles, which are to be distributed in 2 boxes, then there will be 'n+1' macrostates.
(4) Microstate
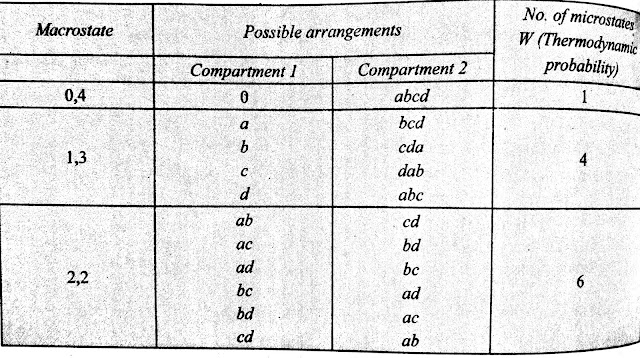
Let us take one Macrostate (1,3) from the above exmaple. It means that there is 1 particles in box 1 and 3 particles in box 2. The four particles are named as a,b,c and d.
Now the one which is in the box 1 can be a, b, c or d.
And the three particles which are in box 2 can be abc, bcd, abd and acd.
Hence microstate of the system is the state in which we consider the arrangement of the individual particles of the system. It can not be experimentally observed.
Possible arrangements for the above exmaple is given below in tables-
 |
| Table for number of microstates |
Now from above table we can say that the total number of microstate for the system that we have taken in the above exmaple is 1+4+6+4+1=16
If there are 'n' particles , distributed in 2 boxes, then the number of microstates will be 2n.
(5) Thermodynamic Probability
The number of microstates corresponding to any given macrostate is called its thermodynamic Probability. It is denoted by W(or Ω).
Let us take the above given exmaple. We have to calculate thermodynamic probability for the Macrostate (1,3). In the above table we can observe that the number of microstates corresponding to the macrostate (1,3) is 4.
Hence the thermodynamic probability for the macrostate (1,3) is 4.
Therefore, W(1,3) = 4
If the total number of particles is 'n' and the macrostate is (r, n-r), then we will use combination to find the number of arrangements. i.e. ,
Now, the number of meaningful arrangements is equal to the number of microstates and the number of microstates is equal to thermodynamic Probability.
Therefore the thermodynamic Probability for the macrostate (r, n-r) can be given by
Therefore the thermodynamic Probability for the macrostate (r, n-r) can be given by
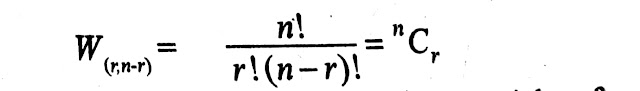 |
| Thermodynamic Probability for Macrostate (r, n-r) |
(6) Constraints
A set of conditions or restrictions that must be obeyed by a system are known as constraints.
Some typical constraints are-
1) Constant number of particles
2) Constant total energy
Which can be written in mathematical form as:
The micro States which are allowed under the given restrictions or constraints of the system are called accessible microstates.
On the other hand, the microstates which do not obey the given constraints are not allowed and they are called the non-accessible microstates.
PRINCIPLE OF EQUAL A PRIORI PROBABILITY
Suppose we toss a coin, then the Probability of head and tail is equal. We can assume before the experiment that the probability of coming head is equal to that of coming a tail.
The principle of assuming equal probability for events which are equally likely to occur is known as the Principle of equal a priori probability.
Or
The Probability of each of the accessible microstates corresponding to a given macrostate is same.
PROBABILITY OF A MICROSTATE
To find the probability of a microstate, we will use the principle of equal a priori probability. Hence probability of each accessible microstate is equal.
Probability of a microstate= 1/(total number of microstate)
Let it be p, thereforep= 1/(total number of microstates)
PROBABILITY OF A MACROSTATE
The probability of a macrostate is defined as the ratio of (number of accessible microstates corresponding to the given macrostate) thermodynamic probability to the total number of microstates.
Let it be P, therefore
P = (thermodynamic probability)/(total number of microstates)
OrP = W/p
where W is thermodynamic probability of that macrostate and p is the probability of a microstate.
Click on the sidemenu and follow the blog!
Click on subscribe button for email subscription.
Share your feedback down in the comment box.
Click on subscribe button for email subscription.
Share your feedback down in the comment box.
Thanks for reading!
Our facebook page- KnowPhysics facebook page
Our Quora space - KnowPhysics Quora
Our facebook page- KnowPhysics facebook page
Our Quora space - KnowPhysics Quora


Very nice post. Thank you.
ReplyDeleteTNPSC Current Affairs in Tamil
tnpsc question paper
samacheer kalvi books
tnpsc group 1 exams
emis number